Statistical and computational physics of biomolecular systems

Anomalous relaxation and diffusion processes in biomolecular systems
The internal dynamics of biomolecular systems such as proteins is characterized by a vast spectrum of time scales and most of the dynamical modes are strongly overdamped and diffusive. Their time evolution and corresponding time correlation functions can be modeled by fractional Fokker-Planck equations, which generalize the idea of Markovian, i.e. memoryless small-step diffusion processes to stochastic processes with long-time memory. The keyword “anomalous relaxation” refers here to the strongly non-exponential decay of the corresponding time correlation functions. We have successfully applied and continue to apply such concepts to model quasielastic neutron scattering spectra and NMR relaxation spectra from proteins.
Anomalous diffusion generally refers to unconstrained diffusion process where the mean square displacement exhibits a non-linear growth with time. The underlying mechanisms are the same as for anomalous relaxation, except that the dynamics of the diffusing particles, which maybe anything from single atoms to whole proteins, is not space-limited. We have studied anomalous lateral diffusion if lipid molecules in lipid bilayers and we have also developed a theoretical framework for anomalous diffusion and relaxation in general, which links such processes to the atomistic dynamics in “crowded” molecular systems. Anomalous diffusion is an ubiquitous phenomenon which is also of great importance in other domains of science, such as in solid state physics, in physical chemistry, and in financial mathematics (http://www.smoluchowski.if.uj.edu.pl).
Minimal models for protein structure and dynamics
Based on the concepts of fractional Brownian dynamics and on the general theoretical framework for anomalous diffusion and relaxation processes, we have developed a so-called minimal model for the backbone dynamics of proteins (J. Chem. Phys. Editor’s choice 2012) and more recently a model-free interpretation of quasielastic neutron scattering spectra (QENS) from proteins proteins (J. Chem. Phys. Editor’s choice 2016). The basic features of protein dynamics, in particular its multiscale character, is here captured by essentially two parameters describing, respectively, the form and the scale of a spectrum. In case of the QENS analysis one uses in addition that high-resolution spectrometers can only detect the asymptotic for of the dynamics for long times and small frequencies.
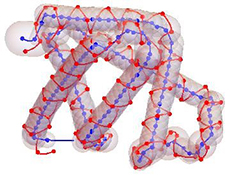
Another type of minimal protein models, which has been developed in the team, concerns the bigactad.gifcharacterization of their global fold. The ScrewFrame model uses the positions of the Cα-atoms along the backbone of a protein to construct a tube model for the protein under consideration. Such a tube model is essentially characterized by the bending and by the internal torsion of the tube. The model is based on Cα-based Frenet frames, which are constructed from the discrete trace of the Cα-positions, and a sequence of helix motions relating these frames. Current applications concern the structural characterization of “unstructured proteins” and the analysis of electron microscopy clichés.
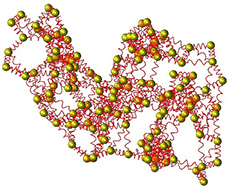
Elastic Network Models for proteins
An Elastic Network Model (ENM) describes a protein as a structured elastic object at a coarse-grained level. The most widely used ENMs represent a protein by its Cα atoms connected by springs. We have been developing, evaluating, and applying ENMs for many years, with applications including in particular the interpretation of low-resolution protein structures and the analysis of conformational transitions.
Reproducible research
The rapid change in computing technology have made it difficult to reproduce or verify results obtained with the help of computers. The publication of software and electronic datasets are crucial to improve to make such research transparent, but it remains difficult to publish them in such a way that other scientists can easily re-run a computational analysis several years later. We have been publishing most of our work reproducibly in recent years, using the ActivePapers framework that we are developing to support the specific needs of biomolecular simulation.
Scientific data management
A major technical challenge in publishing biomolecular simulation data is the lack of suitable file formats for many data types. Only molecular configurations and sequences of such configurations (trajectories) are well supported by today’s software tools. Other important information, such as molecular systems definitions, including force fields and their parameters, normal modes, or models used in trajectory analysis, are difficult to archive or exchange, and are therefore not published at all. We are working on the development of modular and extensible data model and file formats for all aspects of molecular simulation. Current projects in this field are the MOSAIC data model and the digital scientific notation Leibniz.
We use Pharo for these projetcs.
Software development
Most of our research is methodological and therefore requires the development of appropriate software. We have made all our research software publicly available, both to allow verification of our work and to provide useful tools to the scientific community. Our most widely used tools are the Molecular Modelling Toolkit (MMTK), a Python library for molecular simulation, and nMOLDYN, an analysis tool for Molecular Dynamics (MD) trajectories and the calculation of MD-based neutron scattering spectra.

